Ashish Katiyar

Ashish Katiyar

PhD. Student DICE Track ECE Department University of Texas at Austin

Robust Estimation of Tree Structured Gaussian Graphical Models

Introduction and Background:

Graphical models are a way of efficiently representing the joint conditional independence relationships satisfied by a collection of random variables. The nodes of the graph are the random variables. The absence of an edge between 2 nodes encodes that conditioning on the remaining random variables, the 2 random variables are independent (Example in Figure 1). For jointly Gaussian random variables, the graphical model is given by the non-zeros in the inverse covariance matrix (precision matrix) (Example in Figure 1). If the random variables have noise, the conditional independence structure would break down (Example in Figure 2). We address problem of recovering the underlying conditional independence structure when there is independent noise in the random variables given that the graphical model is a tree. 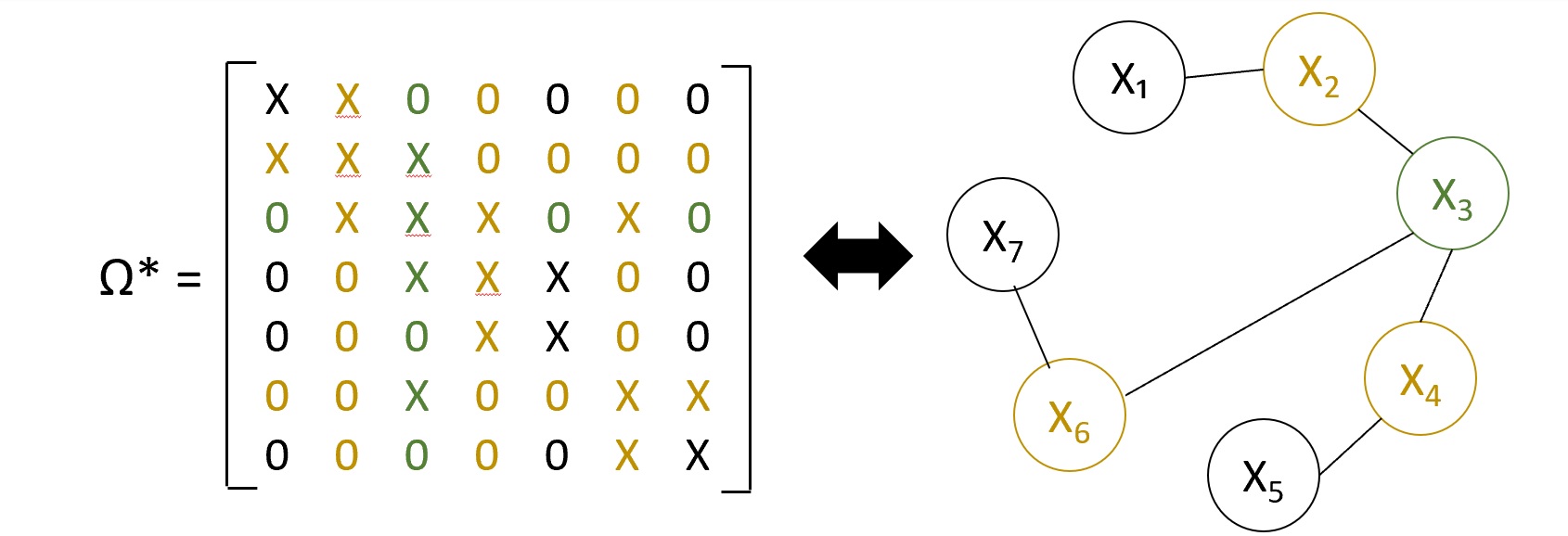Figure 1 Figure 1: For jointly Gaussian random variables zeros in inverse covariance imply absence of edge. X-Non zero elements 0-Zero Elements. Example independence relation - $X_3 \perp X_1, X_5, X_7 | X_2, X_4, X_6$

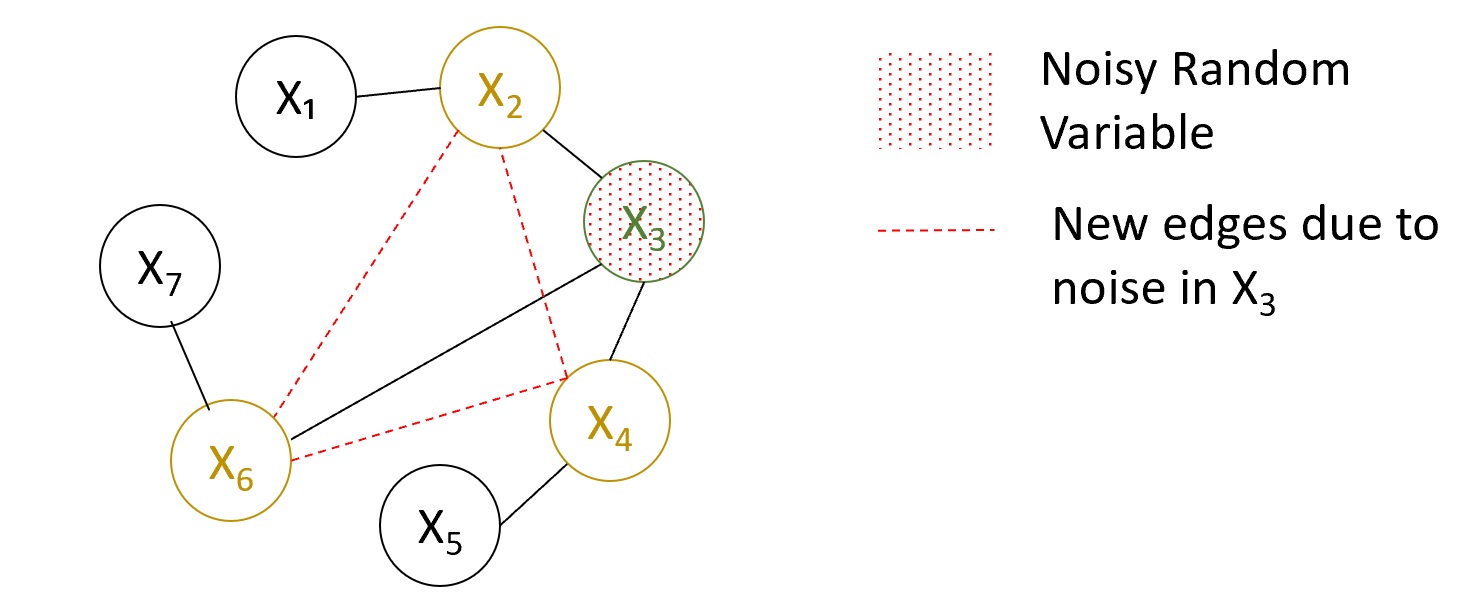Figure 2 Figure 2: Noise in X3 breaks down the conditional independence structure of a subset of the nodes which gives rise to new edges.

Problem Setup

Let $X$ be a vector of zero mean jointly Gaussian random variables whose conditional independence structure is given by a tree $T^* $. Let the covariance matrix of $X$ be $\Sigma^* $ and the precision matrix be $\Omega^* =(\Sigma^* )^{-1} $. As an input we have $\Sigma^o = \Sigma^* + D^* $ where $D^* $ is a positive diagonal matrix corresponding to the noise. Ideally we would like to recover the tree structure $T^* $ (Figure 3).

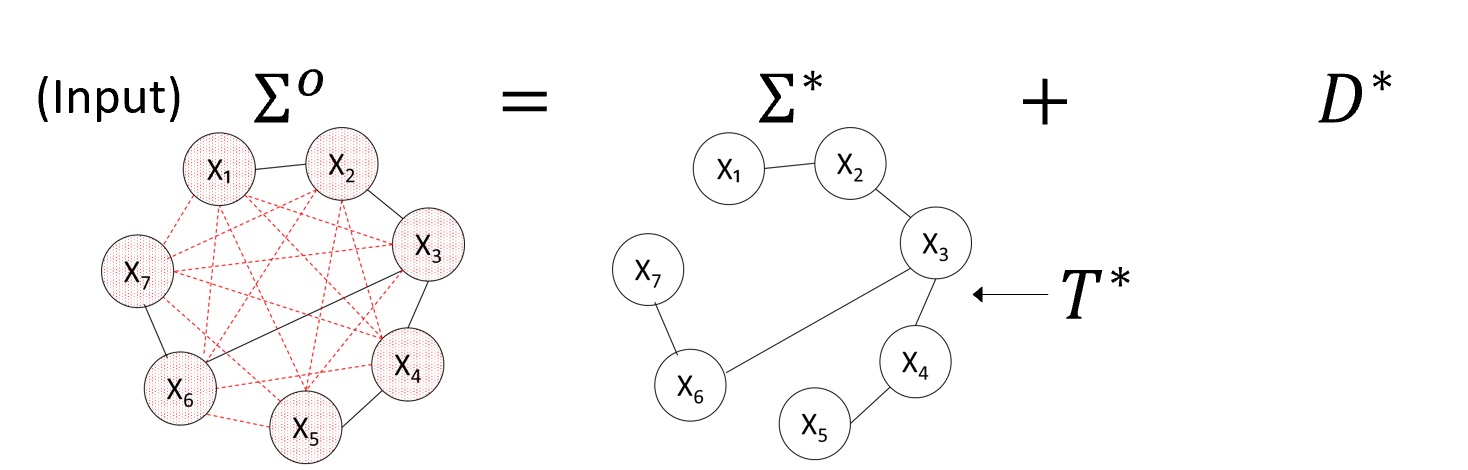Figure 3 Figure 3: Desired decomposition

Results

A negative result: The problem is unidentifiable even in the simple case of 3 nodes with small amount of independent noise.

A positive result: The ambiguity in tree structure is highly limited. The only ambiguity is between a leaf node and its immediate parent. (Figure 4)

Additional constraints for identifiability: We characterize a threshold such that if, as side information, we know that the noise is upper bounded by this threshold, then the original graph is exactly identifiable.

Algorithm: We provide an $\mathcal{O}(n^3)$ algorithm to find the underlying tree structure given the noisy covariance matrix $\Sigma^o $ as an input. We follow a recursive approach where we find a subset of the nodes which form a subtree and the node in the subtree which connects to the rest of the tree at each recursive step. (Figure 5)

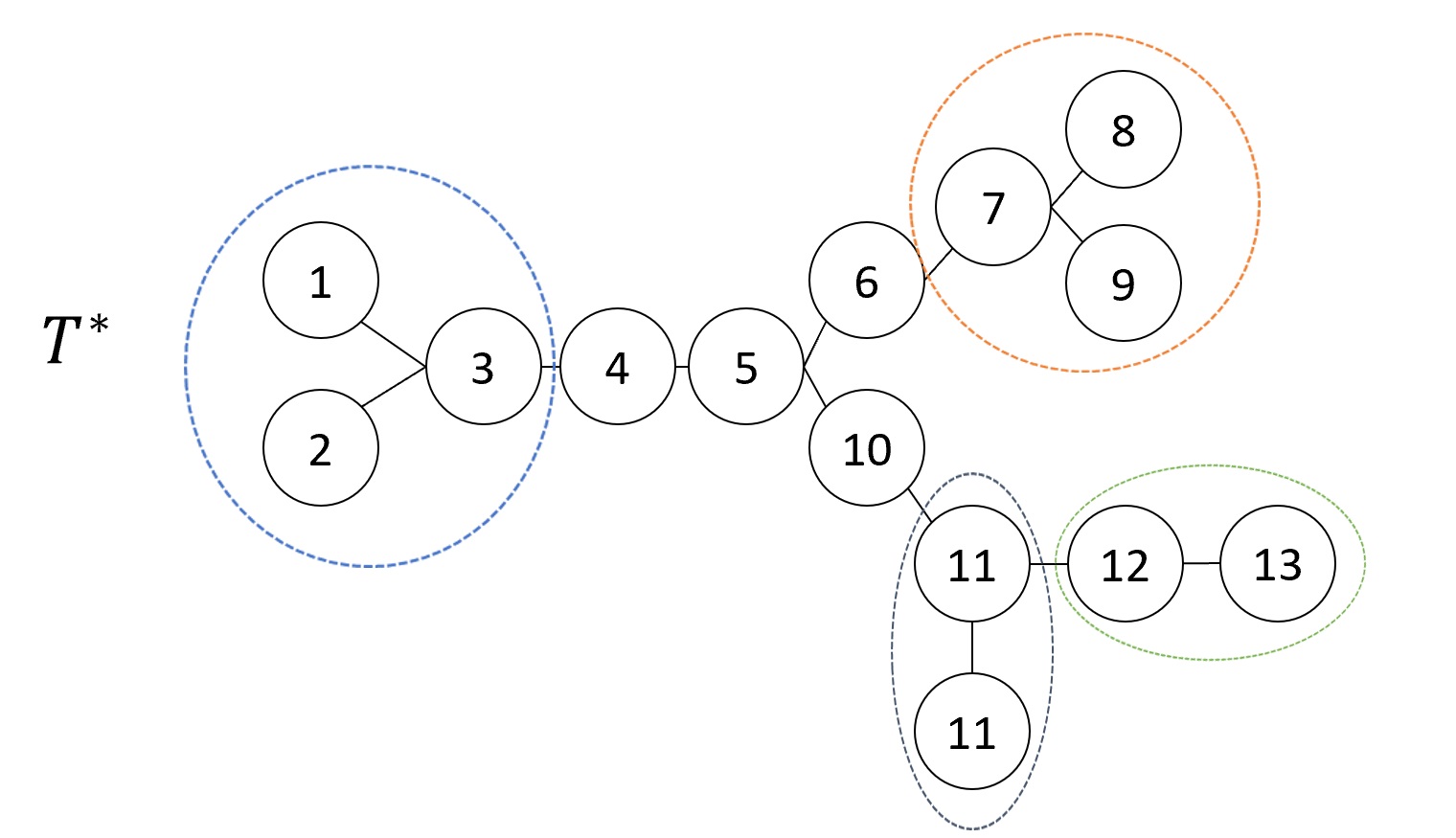Figure 4 Figure 4: For the above tree $T^* $, any unidentifiability is limited to the permutation of the nodes within each dotted region. 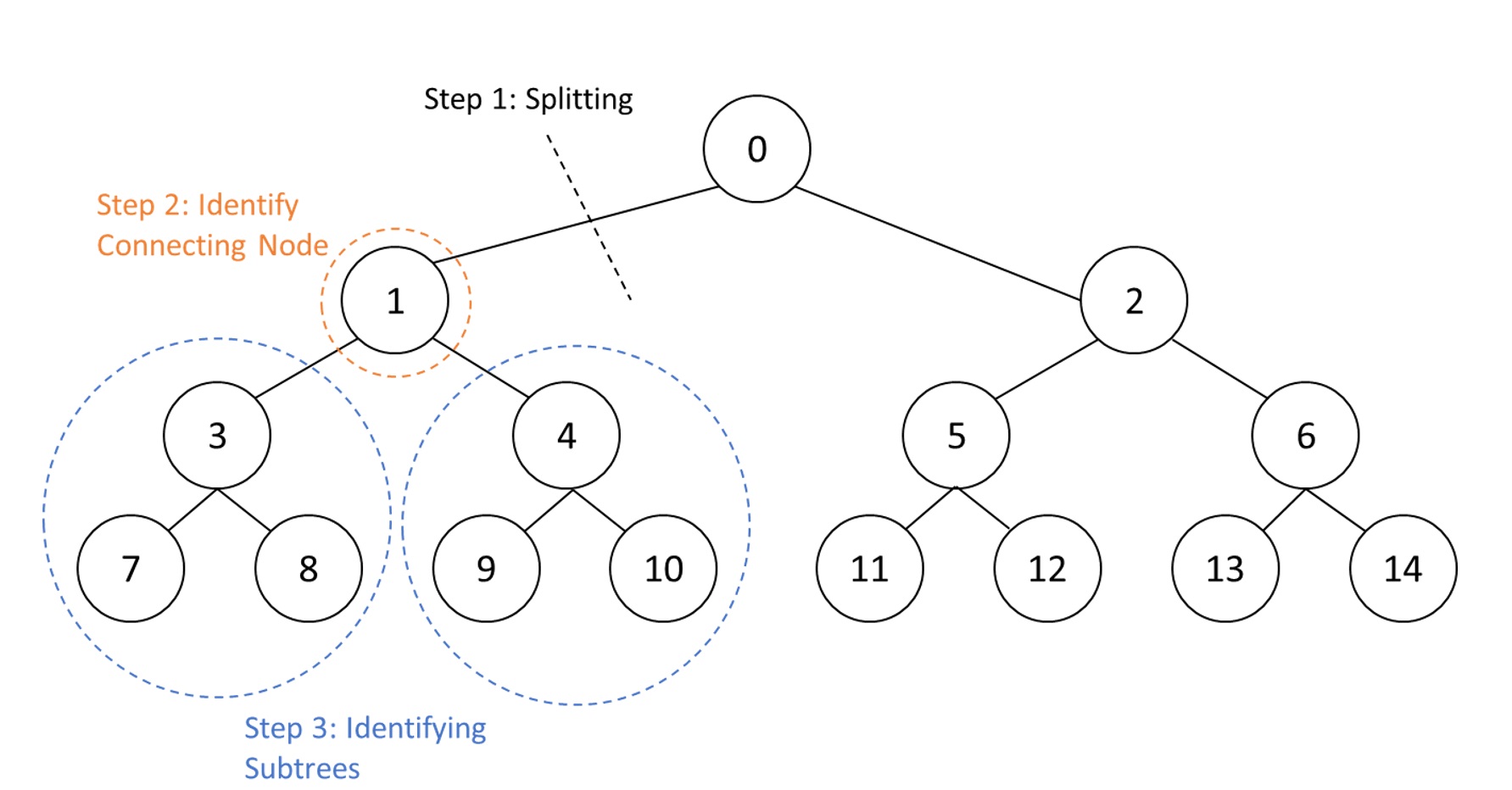Figure 5 Figure 5: The steps taken by the algorithm recursively.